Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym :

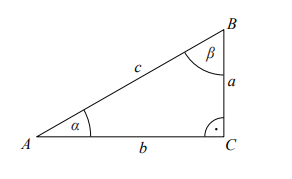sin α	=	a
		c
cos α	=	b
		c
tg α	=	a
		b

Definicje funkcji trygonometrycznych

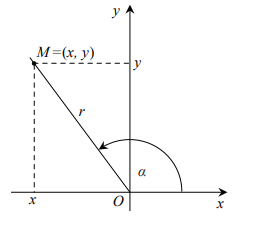sin α	=	y
		r
cos α	=	x
		r
tg α	=	y	gdy x ≠ 0
		x

gdzie r =√x² + y² > 0 jest

promieniem wodzącym punktu M

Wykresy funkcji trygonometrycznych

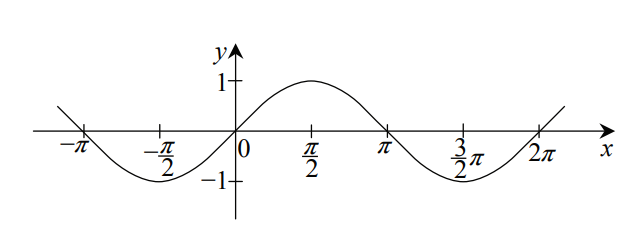y = sin x	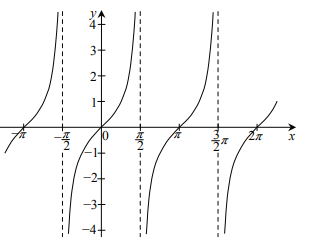y = tg x
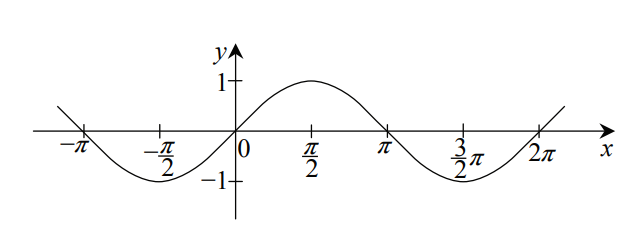y = cos x

Związki między funkcjami tego samego kąta

sin 2 α + cos 2 α = 1
tg α =	sin α	dla      α ≠ α =	π	+ k π,         k - całkowite
	cos α		2

Niektóre wartości funkcji trygonometrycznych

α	0 °	30°	45°	60°	90°
	0	π	π	π	π
		6	4	3	2
sin α	0	1	√ 2	√3	1
		2	2	2
cos α	1	√3	√ 2	1	0
		2	2	2
tg α	0	√3	1	√3	nie istnieje
		2	2

Funkcje sumy i różnicy kątów

Dla dowolnych kątów α, β zachodzą równości:

sin (α+ β) = sin α cos β + cos α sinβ	sin (α- β) = sin α cos β - cos α sinβ
cos (α- β) = cos α cos β - sin α sinβ	cos (α+ β) = cos α cos β + sin α sinβ

Ponadto mamy równośći

tg (α+ β) =	tg α + tg β	tg (α- β) =	tg α - tg β
	1- tg α * tg β		1+ tg α * tg β

które zachodzą zawsze, gdy są określone i mianownik prawej strony nie jest zerem.

Funkcje podwojonego kąta

sin 2 α = 2sin α cos α

cos 2 α = cos 2 α - sin 2 α = 2 cos 2 α -1 = 1 - 2 sin 2 α

tg 2 α =	2 tg α
	1 - tg 2 α

Sumy, różnice i iloczyny funkcji trygonometrycznych

sin α + sin β = 2 sin	α + β	cos	α - β	sin α sin β = -	1	(cos(α + β) - cos (α - β))
	2		2		2
sin α - sin β = 2 sin	α + β	cos	α - β	cos α cos β =	1	(cos(α + β) + cos (α - β))
	2		2		2
cos α + cos β = 2 sin	α + β	cos	α - β	sin α cos β = -	1	(sin(α + β) - cos (α - β))
	2		2		2
cos α + cos β = -2 sin	α + β	cos	α - β
	2		2

Wybrane wzory redukcyjne

sin ( 90° - α ) = cos α	cos ( 90° - α ) = sin α
sin ( 90° + α ) = cos α	cos ( 90° + α ) = -sin α
sin ( 180° - α ) = sin α	cos ( 180° - α ) = -cos α	tg(180° - α) = -tg α
sin ( 180° + α ) = -sin α	cos ( 180° + α ) = -cos α	tg(180° + α) = tg α

Okresowość funkcji trygonometrycznych

sin ( a + k * 360°) = sin α

cos ( a + k * 360°) = cos α

tg ( a + k * 360°) = tg α

k - całkowite