• Cechy przystawania trójkątów
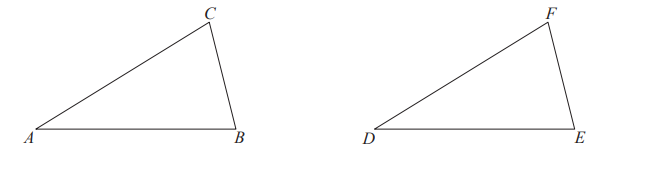To, że dwa trójkąty ABC i DEF są przystające (∆ABC ≡ ∆DEF) , możemy stwierdzić na podstawie każdej
z następujących cech przystawania trójkątów:
– cecha przystawania „bok – bok – bok”:
odpowiadające sobie boki obu trójkątów mają te same długości: |AB|=|DE|, |AC|=|DF|, |BC|=|EF|
– cecha przystawania „bok – kąt – bok”: dwa boki jednego trójkąta są równe odpowiadającym im bokom drugiego trójkąta oraz kąt zawarty między tymi bokami jednego trójkąta ma taką samą miarę jak odpowiadający mu kąt drugiego trójkąta, np. |AB|=|DE|, |AC|=|DF|, |∢BAC|=|∢EDF|
– cecha przystawania „kąt – bok – kąt”:
jeden bok jednego trójkąta ma tę samą długość, co odpowiadający mu bok drugiego trójkąta oraz miary odpowiadających sobie kątów obu trójkątów, przyległych do boku, są równe, np. |AB|=|DE|, |∢BAC|=|∢EDF|, |∢ABC|=|∢DEF|
• Cechy podobieństwa trójkątów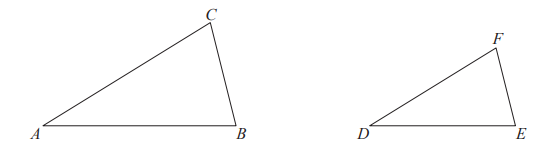
To, że dwa trójkąty ABC i DEF są podobne (∆ABC ∼ ∆DEF) , możemy stwierdzić na podstawie każdej z następujących cech podobieństwa trójkątów:
– cecha podobieństwa „bok – bok – bok”: długości boków jednego trójkąta są proporcjonalne do odpowiednich długości boków drugiego trójkąta, np.
– cecha podobieństwa „bok – kąt – bok”: długości dwóch boków jednego trójkąta są proporcjonalne do odpowiednich długości dwóch boków drugiego trójkąta i kąty między tymi parami boków są przystające, np.
– cecha podobieństwa „kąt – kąt – kąt”: dwa kąty jednego trójkąta są przystające do odpowiednich dwóch kątów drugiego trójkąta (więc też i trzecie kąty obu trójkątów są przystające): |∢BAC|=|∢EDF|, |∢ABC|=|∢DEF|, |∢ACB|=|∢DFE|
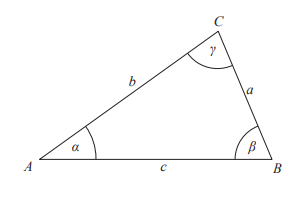
• Wzory na pole trójkąta
• Twierdzenie Pitagorasa (wraz z twierdzeniem odwrotnym do niego) W trójkącie ABC kąt γ jest prosty wtedy i tylko wtedy, gdy a2+b2=c2
• Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego) Różne proste AC i BD przecinają się w punkcie P, przy czym spełniony jest jeden z warunków: – punkt A leży wewnątrz odcinka PC oraz punkt B leży wewnątrz odcinka PD lub – punkt A leży na zewnątrz odcinka PC oraz punkt B leży na zewnątrz odcinka PD. Wówczas proste AB i CD są równoległe wtedy i tylko wtedy, gdy
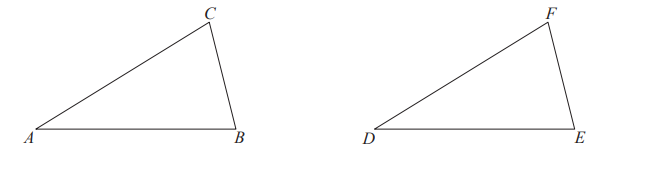To, że dwa trójkąty ABC i DEF są przystające (∆ABC ≡ ∆DEF) , możemy stwierdzić na podstawie każdej
z następujących cech przystawania trójkątów:– cecha przystawania „bok – bok – bok”:
odpowiadające sobie boki obu trójkątów mają te same długości: |AB|=|DE|, |AC|=|DF|, |BC|=|EF|
– cecha przystawania „bok – kąt – bok”: dwa boki jednego trójkąta są równe odpowiadającym im bokom drugiego trójkąta oraz kąt zawarty między tymi bokami jednego trójkąta ma taką samą miarę jak odpowiadający mu kąt drugiego trójkąta, np. |AB|=|DE|, |AC|=|DF|, |∢BAC|=|∢EDF|
– cecha przystawania „kąt – bok – kąt”:
jeden bok jednego trójkąta ma tę samą długość, co odpowiadający mu bok drugiego trójkąta oraz miary odpowiadających sobie kątów obu trójkątów, przyległych do boku, są równe, np. |AB|=|DE|, |∢BAC|=|∢EDF|, |∢ABC|=|∢DEF|
• Cechy podobieństwa trójkątów
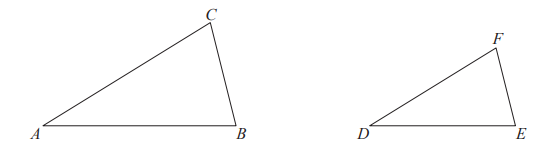
To, że dwa trójkąty ABC i DEF są podobne (∆ABC ∼ ∆DEF) , możemy stwierdzić na podstawie każdej z następujących cech podobieństwa trójkątów:
– cecha podobieństwa „bok – bok – bok”: długości boków jednego trójkąta są proporcjonalne do odpowiednich długości boków drugiego trójkąta, np.
| |AB| | = | |AC| | = | |BC| |
| |DE| | |DF| | |EF| |
– cecha podobieństwa „bok – kąt – bok”: długości dwóch boków jednego trójkąta są proporcjonalne do odpowiednich długości dwóch boków drugiego trójkąta i kąty między tymi parami boków są przystające, np.
| |AB| | = | |AC| | , | |∢BAC| | = | |∢EDF| |
| |DE| | |DF| |
– cecha podobieństwa „kąt – kąt – kąt”: dwa kąty jednego trójkąta są przystające do odpowiednich dwóch kątów drugiego trójkąta (więc też i trzecie kąty obu trójkątów są przystające): |∢BAC|=|∢EDF|, |∢ABC|=|∢DEF|, |∢ACB|=|∢DFE|
• Przyjmujemy oznaczenie w trójkącie ABC:
a, b, c –długości boków, leżących odpowiednio naprzeciwko wierzchołków A, B, C
2p=a+b+c –obwód trójkąta
α, β, γ –miary kątów przy wierzchołkach A, B, C
ha,hb,hc –wysokości opuszczone z wierzchołków A, B, C
R,r – promienie okręgów opisanego i wpisanego
a, b, c –długości boków, leżących odpowiednio naprzeciwko wierzchołków A, B, C
2p=a+b+c –obwód trójkąta
α, β, γ –miary kątów przy wierzchołkach A, B, C
ha,hb,hc –wysokości opuszczone z wierzchołków A, B, C
R,r – promienie okręgów opisanego i wpisanego
• Twierdzenie sinusów
| a | = | b | = | c | = | 2R |
| sinα | sinβ | sinγ |
• Twierdzenie cosinusów
a2=b2+c2-2bc cosα
b2=a2+c2-2bc cosβ
c2=a2+n2-2bc cosγ
a2=b2+c2-2bc cosα
b2=a2+c2-2bc cosβ
c2=a2+n2-2bc cosγ
• Wzory na pole trójkąta
| P∆ABC | = | 1 | ×a×ha | = | 1 | ×b×hb | = | 1 | ×c×hc |
| 2 | 2 | 2 |
| P∆ABC | = | 1 | ×a×ba×sinγ | = | 1 | a×c×sinβ | = | 1 | b×c×sinα |
| 2 | 2 | 2 |
| P∆ABC | = | 1 | ×a2× | sinβ×sinγ | = | 1 | b2× | sinα×sinγ | = | 1 | c2× | sinα×sinβ |
| 2 | sinα | 2 | sinβ | 2 | sinγ |
| P∆ABC | = | abc |
| 4R |
| P∆ABC | = | 2R2×sinα ×sinβ ×sinγ |
| P∆ABC | = | rp |
| P∆ABC | = | √p(p−a)(p−b)(p−c) |
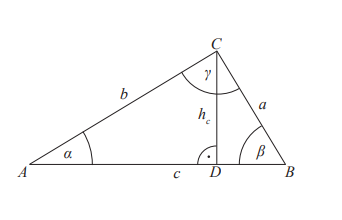
• Twierdzenie Pitagorasa (wraz z twierdzeniem odwrotnym do niego) W trójkącie ABC kąt γ jest prosty wtedy i tylko wtedy, gdy a2+b2=c2
• Związki miarowe w trójkącie prostokątnym
Załóżmy, że kąt γ jest prosty. Wówczas:
hc2=|AD|×|DB|
a=c×sinα =c×cosβ
Załóżmy, że kąt γ jest prosty. Wówczas:
hc2=|AD|×|DB|
| hc= | = | ab |
| c |
| a=b × tgα = b× | 1 |
| tgβ |
| R= | 1 | c |
| 2 |
| r= | a+b−c | =p−c |
| 2 |
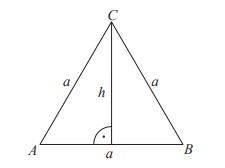
• Trójkąt równoboczny
a -długość boku
h -wysokość trójkąta
a -długość boku
h -wysokość trójkąta
| h | = | a√3 |
| 2 |
| P∆ = | a2√3 |
| 4 |
| R= | 2 | h |
| 3 |
| r= | 1 | h |
| 3 |
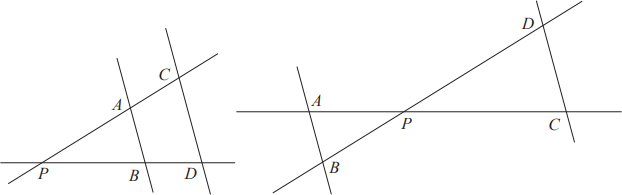
• Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego) Różne proste AC i BD przecinają się w punkcie P, przy czym spełniony jest jeden z warunków: – punkt A leży wewnątrz odcinka PC oraz punkt B leży wewnątrz odcinka PD lub – punkt A leży na zewnątrz odcinka PC oraz punkt B leży na zewnątrz odcinka PD. Wówczas proste AB i CD są równoległe wtedy i tylko wtedy, gdy
| |PA| | = | |PB| |
| |AC| | |BD| |