• Koło

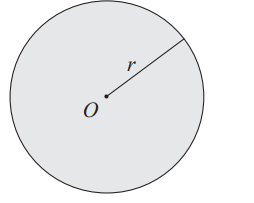
Wzór na pole koła o promieniu r:
P = π r ²

---

• Wycinek Koła

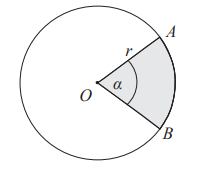
Wzór na pole wycinka koła o promieniu r i kącie środkowym α wyrażonym w stopniach:

P = π r 2 *	α
	360°

Długość łuku AB wycinka koła o promieniu r i kącie środkowym α wyrażonym w stopniach:

---

• Kąty w Okręgu

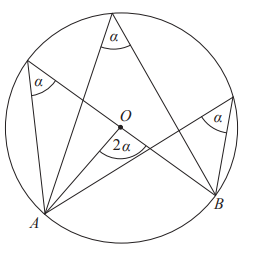
Miara kąta wpisanego w okrąg jest równa połowie miary kąta środkowego, opartego na tym samym łuku.

Miary kątów wpisanych w okrąg, opartych na tym samym łuku, są równe.

Miary kątów wpisanych w okrąg, opartych na łukach równych, są równe.

---

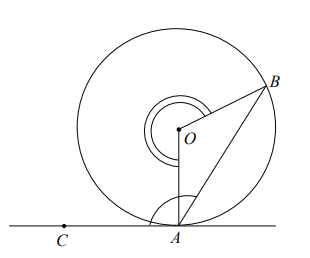
• Twierdzenie o kącie między styczną i cięciwą

Dany jest okrąg o środku w punkcie O i jego cięciwa AB. Prosta AC jest styczna do tego okręgu w punkcie A. Wtedy | ∢ AOB | = 2 × | ∢ AB | , przy czym wybieramy ten z kątów środkowych AOB, który jest oparty na łuku znajdującym się wewnątrz kąta CAB.

---

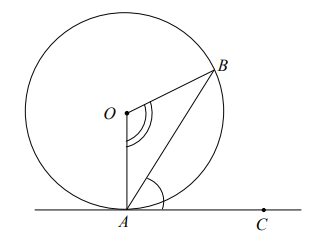
• Twierdzenie o odcinkach stycznych

Jeżeli styczne do okręgu w punktach A i B przecinają się w punkcie P, to :

|PA| = |PB|

---

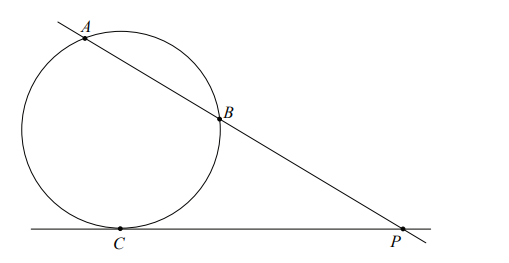
• Twierdzenie o odcinkach siecznej i stycznej

Dane są: prosta przecinająca okrąg w punktach A i B oraz prosta styczna do tego okręgu w punkcie C. Jeżeli proste te przecinają się w punkcie P, to

|PA| × |PB| = |PC| ²

---

• Okrąg opisany na czworokącie

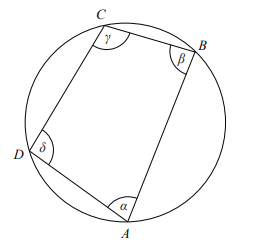
Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów wewnętrznych są równe 180°:

α + γ = β + δ = 180°

---

• Okrąg wpisany na czworokącie

W czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy sumy długości jego przeciwległych boków są równe:

a + c = b + d