* Odcinek
Długość odcinka o końcach w punktach A=(xA,yA), B=(xB,yB) jest dana wzorem:
|AB|=√(xB-xA)2, (yB-yA)2
Współrzędne środka odcinka AB:
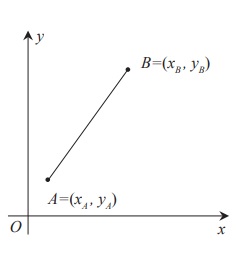
* Wektory
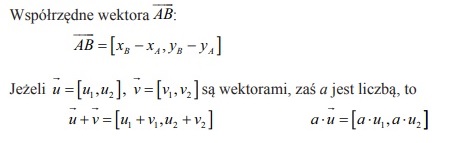* Prosta
Równanie ogólne prostej: Ax+By+C = 0,
gdzie A2+B2 ≠ 0 (tj. współczynniki A, B nie są równocześnie równe 0).
Jeżeli A = 0, to prosta jest równoległa do osi OX; jeżeli B = 0, to prosta jest równoległa do osi OY;
jeżeli C = 0, to prosta przechodzi przez początek układu współrzędnych.
Jeżeli prosta nie jest równoległa do osi Oy, to ma ona równanie kierunkowe:
y=a+x b
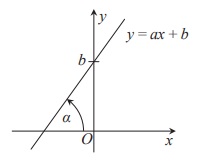
Liczba a to współczynnik kierunkowy prostej:
a = tg α
Współczynnik b wyznacza na osi OY punkt, w którym dana prosta ją przecina.
Równanie kierunkowe prostej o współczynniku kierunkowym a, która przechodzi przez punkt P=(x0,y0)
y=a(x-x0)+y0
Równanie prostej, która przechodzi przez dwa dane punkty
A=(xA,yA), B=(xB,yB) to:
(y-yA)(xB-xA)-(yB-yA)(x-xA)=0
* Prosta i punkt
Odległość punktu P=(x0,y0) od prostej o równaniu Ax+By+C =0 jest dana wzorem:
* Para prostych
Dwie proste o równaniach kierunkowych:
spełniają jeden z następujących warunków:
- są równoległe, gdy a1=a2
– są prostopadłe, gdy a1a2=-1
Dwie proste o równaniach ogólnych:
– są równoległe, gdy A1B2-A2B1=0
– są prostopadłe, gdy A1A2-B1B2=0
* Trójkąt
Pole trójkąta ABC o wierzchołkach A=(xA,yA), B=(xB,yB), C=(xC,yC), jest dane wzorem:
P∆ABC=½|(xB-xA)(yC-yA)-(yB-yA)(xC-xA)|
Środek ciężkości trójkąta ABC, czyli punkt przecięcia jego środkowych, ma współrzędne:
* Przekształcenia geometryczne
– przesunięcie o wektor u¯=[a,b]przekształca punkt A=(x,y) na punkt A'=(x+a,y+b)
– symetria względem osi Ox przekształca punkt A=(x,y) na punkt A'=(x,-y)
– symetria względem osi Oy przekształca punkt A=(x,y) na punkt A'=(-x,y)
– symetria względem punktu (a,b) przekształca punkt A=(x,y)na punkt A'=(2a-x,2b-y)
– jednokładność o środku w punkcie O i skali s≠0 przekształca punkt A na punkt A' taki, że
OA¯'=s×OA¯, a więc, jeśli O=(x0,y0), to jednokładność ta przekształca punkt A=(x,y) na punkt
A'=(sx+(1-s)x0,sy+(1-s)y0)
* Równanie okręgu
Równanie okręgu o środku w punkcie S=(a,b) i promieniu r>0:
(x-a)2+(y-b)2=r2
lub x2+y2-2ax-2by+c=0 gdy r2=a2+b2-c>0
Długość odcinka o końcach w punktach A=(xA,yA), B=(xB,yB) jest dana wzorem:
|AB|=√(xB-xA)2, (yB-yA)2
Współrzędne środka odcinka AB:
| ( | xA+ xB | xA+ xB |
| 2 | 2 | ) |
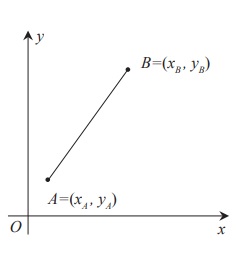
* Wektory
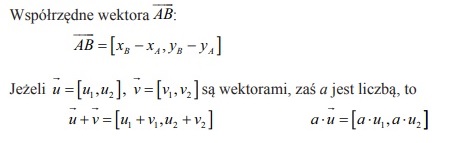* Prosta
Równanie ogólne prostej: Ax+By+C = 0,
gdzie A2+B2 ≠ 0 (tj. współczynniki A, B nie są równocześnie równe 0).
Jeżeli A = 0, to prosta jest równoległa do osi OX; jeżeli B = 0, to prosta jest równoległa do osi OY;
jeżeli C = 0, to prosta przechodzi przez początek układu współrzędnych.
Jeżeli prosta nie jest równoległa do osi Oy, to ma ona równanie kierunkowe:
y=a+x b
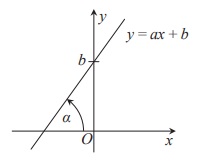
Liczba a to współczynnik kierunkowy prostej:
a = tg α
Współczynnik b wyznacza na osi OY punkt, w którym dana prosta ją przecina.
Równanie kierunkowe prostej o współczynniku kierunkowym a, która przechodzi przez punkt P=(x0,y0)
y=a(x-x0)+y0
Równanie prostej, która przechodzi przez dwa dane punkty
A=(xA,yA), B=(xB,yB) to:
(y-yA)(xB-xA)-(yB-yA)(x-xA)=0
* Prosta i punkt
Odległość punktu P=(x0,y0) od prostej o równaniu Ax+By+C =0 jest dana wzorem:
| |Ax0+By0+C| | |
| √A2+B2 |
* Para prostych
Dwie proste o równaniach kierunkowych:
| y=a1x+b1 | y=a2x+b2 |
|---|
spełniają jeden z następujących warunków:
- są równoległe, gdy a1=a2
– są prostopadłe, gdy a1a2=-1
| = | a1-a2 | |
| – tworzą kąt ostry φ i tgφ | |
|
| 1+a1a2 |
Dwie proste o równaniach ogólnych:
| A1x+B1y+C1=0 | A2x+B2y+C2=0 |
|---|
– są równoległe, gdy A1B2-A2B1=0
– są prostopadłe, gdy A1A2-B1B2=0
| = | A1B2-A2B1 | |
| – tworzą kąt ostry φ i tgφ | |
|
| A1A2-B1B2 |
* Trójkąt
Pole trójkąta ABC o wierzchołkach A=(xA,yA), B=(xB,yB), C=(xC,yC), jest dane wzorem:
P∆ABC=½|(xB-xA)(yC-yA)-(yB-yA)(xC-xA)|
Środek ciężkości trójkąta ABC, czyli punkt przecięcia jego środkowych, ma współrzędne:
( |
xA+ xB+ xC | yA+ yB+ yC | ) |
|
| 3 | 3 |
* Przekształcenia geometryczne
– przesunięcie o wektor u¯=[a,b]przekształca punkt A=(x,y) na punkt A'=(x+a,y+b)
– symetria względem osi Ox przekształca punkt A=(x,y) na punkt A'=(x,-y)
– symetria względem osi Oy przekształca punkt A=(x,y) na punkt A'=(-x,y)
– symetria względem punktu (a,b) przekształca punkt A=(x,y)na punkt A'=(2a-x,2b-y)
– jednokładność o środku w punkcie O i skali s≠0 przekształca punkt A na punkt A' taki, że
OA¯'=s×OA¯, a więc, jeśli O=(x0,y0), to jednokładność ta przekształca punkt A=(x,y) na punkt
A'=(sx+(1-s)x0,sy+(1-s)y0)
* Równanie okręgu
Równanie okręgu o środku w punkcie S=(a,b) i promieniu r>0:
(x-a)2+(y-b)2=r2
lub x2+y2-2ax-2by+c=0 gdy r2=a2+b2-c>0